Computer Number System
Computer Number System
Number
system:
A set of values used to represent different quantities
is known as Number System. For example, a number system can be used to
represent the number of students in a class or number of viewers watching a
certain TV program etc. The digital computer represents all kinds of data and
information in binary numbers. It includes audio, graphics, video, text and
numbers. The total number of digits used in a number system is called its base
or radix.
Types
of Number System:
Generally number system can be divided into
two types.They are:
1. Non-positional
Number System, and
2. Positional
Number system.
Non-Positional
Number System:
In early days, Human beings counted on
fingers. when ten fingers were not adequate, stones, pebles, or sticks were used
to indicate values. This mathod of counting uses an additive approach or
the Non-positional Number System.In This
system, we have symbols, such as :-
। For 1,।। For 2,।।। For 4,।।।। For 4,।।।।। For 5 etc.
Positional Number System
In a positional Number
System, there are only a few symbols, called digits, and these symbols
represent different values, depending on the position, they occupy in the
number. The value of each digit in such a number is determined by three
considerations. They are:
1.
The digit,
2.
The position of the digit in the number, and
3.
The base of Number System (where base is
defined as the total number of digits available in the number system).
Different Number System:
There have four
different Number Systems. One of them is used in our day to day life and
another three is used as the Computer Number System. The four different Number
System are given below:
01
|
Decimal Number System
Base: 10, Digits Used …0
to 9
|
02
|
Binary Number System
Base: 2, Digits Used…0,1
|
03
|
Octal Number System
Base: 8, Digits Used…0
to 7
|
04
|
Hexadecimal Number
System
Base:16, Digits Used…0
to 9,Latters Used A to F.
|
1-16 Numbers
Decimal
|
Binary
|
Octal
|
Hexadecimal
|
|
0
|
0
|
0
|
0
|
|
01
|
1
|
1
|
1
|
|
02
|
10
|
2
|
2
|
|
03
|
11
|
3
|
3
|
|
04
|
100
|
4
|
4
|
|
05
|
101
|
5
|
5
|
|
06
|
110
|
6
|
6
|
|
07
|
111
|
7
|
7
|
|
08
|
1000
|
10
|
8
|
|
09
|
1001
|
11
|
9
|
|
10
|
1010
|
12
|
A
|
|
11
|
1011
|
13
|
B
|
|
12
|
1100
|
14
|
C
|
|
13
|
1101
|
15
|
D
|
|
14
|
1110
|
16
|
E
|
|
15
|
1111
|
17
|
F
|
|
16
|
10000
|
20
|
10
|
|
Way of Converting Number System decimal from another
base
01.Binary To Decimal
Example 1: 110012=X10
what is the Value of ‘X’ in here?
That means, 110012=2510
Hence, X=25
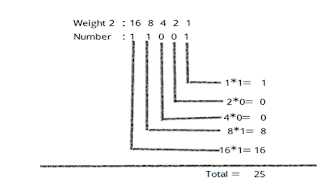
Example 2: 101012=X10,
Here X=?
This Example may more Helpful to you because
it is created by step by step and which is:-
Step 1: Determine the position value of each
digits
Step 2: Multiply the obtained column values by
the digits in the
Corresponding columns.
Step 3: Sum the products calculated in step-2. The total is the
equivalent in Decimal.
That means, 101012=2110
Hence, X=21.
Binary to
Octal
Example 1: 0100111112=X8,
Here ‘X’=?
Step 1: 010 011 111
Step 2:
0102=28
0112=38
1112=78
That means, 0100111112=2378
Hence, X8=237
Binary to Hexadecimal
Example
1: 110100112=X16,
Here ’X’=?
Step 1: 1101 0011
Step 2:
11012=D16
00112=316
Step 3: Count it from up to down=D3
That means, 110100112=D316
Hence, X16=D3
Octal to Binary
Example 1: 5628=X2, Here ‘X’=?
Step 1:
58=1012
68=1102
28=102
Step 2: Count it from up to down = 101 110 010
(Note: if any have less than 3 digits you
should have fulfilled it by set up zero/0 beside its left side. At this site 28=0102)
That means, 5628=1011100102
Hence, X2= 101110010
Octal to Decimal
Example 1: 47068=X10, Here ‘X’ =?
That means, 47068=250210
Hence, X10= 2502
Octal to Hexadecimal
Example 1: 47068=X16, Here X=?
Step 1: Convert these Octal Numbers to Binary…
48=1002
78=1112
08=02
68=1102
Count it
from up to down 47068=1001110001102
(Note: if any have less than 3 digits you
should have fulfilled it by set up zero/0 beside its left side. At this side 08=0002)
Step 2: Convert These Binary Numbers to
Hexadecimal.
1001 1100 01102
10012=916
11002=A16
0110=616
Count it from Up to Down=
9A616
That means, 47068=9A616
Hence, X=9A616
Hexadecimal to Binary
Example 1: 2AB16=X2,
Here X=?
Step 1: 2AB16
216=00102
A16=10102
B16=10112
Step 2: Count it from up to down = 0010101010112
That means, 2AB16= 0010101010112
Hence, X= 0010101010112
(Note: According to Binary from Hexadecimal if any have less than 4
digits you should have fulfilled it by set up zero/0 beside its left side. At
this side 216=00102)
Hexadecimal to Octal
Example 1: ABC16=X8,
Here X=?
Step 1: Convert these numbers from Hexadecimal to Binary
ABC
A16=10102
B16=10112
C16=11002
Count it from Up to Down=
1010101111002
Step 2: Convert These Binary number to Octal
101 010
111 100
1012=58
0102=28
1112=78
1002=48
Count it from Up to Down= 52748
That means, ABC16=52748
Hence, X=52748
Hexadecimal to
Decimal
Example 1: 2AB16=X10,
Here X=?
That means, 2AB16=52910
Hence X=52910
Decimal to Binary
Example 1: 21510=X2,
Here X=?
Step 1: Divide this decimal number by the weight of ‘X’ if any have
Extra,show it right side and if have
not then you should show zero/0.
Step 2: Count it from down to Up= 10101112
That means, 21510=10101112
Hence, X=10101112
Decimal to Octal
Example 1: 19810=X8,
Here X=?
Step 1: Divide this Decimal number by the weight of ‘X’ if any have
Extra,
show it right side and if have
not then you should show zero/0.
Step 2: Count it from down to Up= 3068
That
means, 19810=3068
Hence,
X=3068
Decimal to Hexadecimal
Example 1: 70310=X16,
Here X=?
Step 1: Divide this Decimal number by the weight of ‘X’ if any have
Extra,
show it right side and if have not then you should show zero/0.
Step 2: Count it from down
to Up=2BF16
That means, 70310=2BF16
Hence, X=2BF16
From Self:
Here may have some mistake. Please don’t mind if here have some mistake and
help me to solve those mistake. If hare have any mistake please notice me by
your valuable comments on the comments box or mail me…






মন্তব্যসমূহ